Exploring Recursive Zero-Knowledge Proofs: Understanding How They Verify the Accuracy of Other Proofs
In this article, we will look at Recursive Zero-Knowledge Proofs (ZKP), a type of proof that attests to the validity of other proofs. In simpler terms, it confirms or verifies the truth or accuracy of a proof of a proof of a proof.
Using this example below you’ll be able to understand what a Recursive Proof is
To understand this concept, imagine Lionel Messi the self-acclaimed “GOAT” argues that he’s a better free-kick taker than his rival, Ronaldo and that his free-kicks can reach the back of the net in a shorter time
So, Messi decides to prove to Ronaldo that he can score 5 free kicks in 5 minutes and he decides to prove this using just one picture.
He takes a picture of himself scoring a free-kick in the first minute. In the second minute he does the same thing and repeats this process for the next three minutes.
Now, he has a proof of his free-kick goals in five minutes in one picture.
Digression/ Comic Relief: The Twist (Drama)
The above scenario results in huge media publicity and the pundits praise Messi as the "GOAT". Messi sends the proof to Ronaldo, who feels insecure about it and decides to show it to Piers Morgan.
Piers Morgan then sends it to the Football Association (FA) for further analysis, and it is concluded that the last photo in the proof was actually a penalty and not a free-kick 😂.
The above scenario is a digression and is just for fun, but importantly, I hope you understand the message being conveyed.
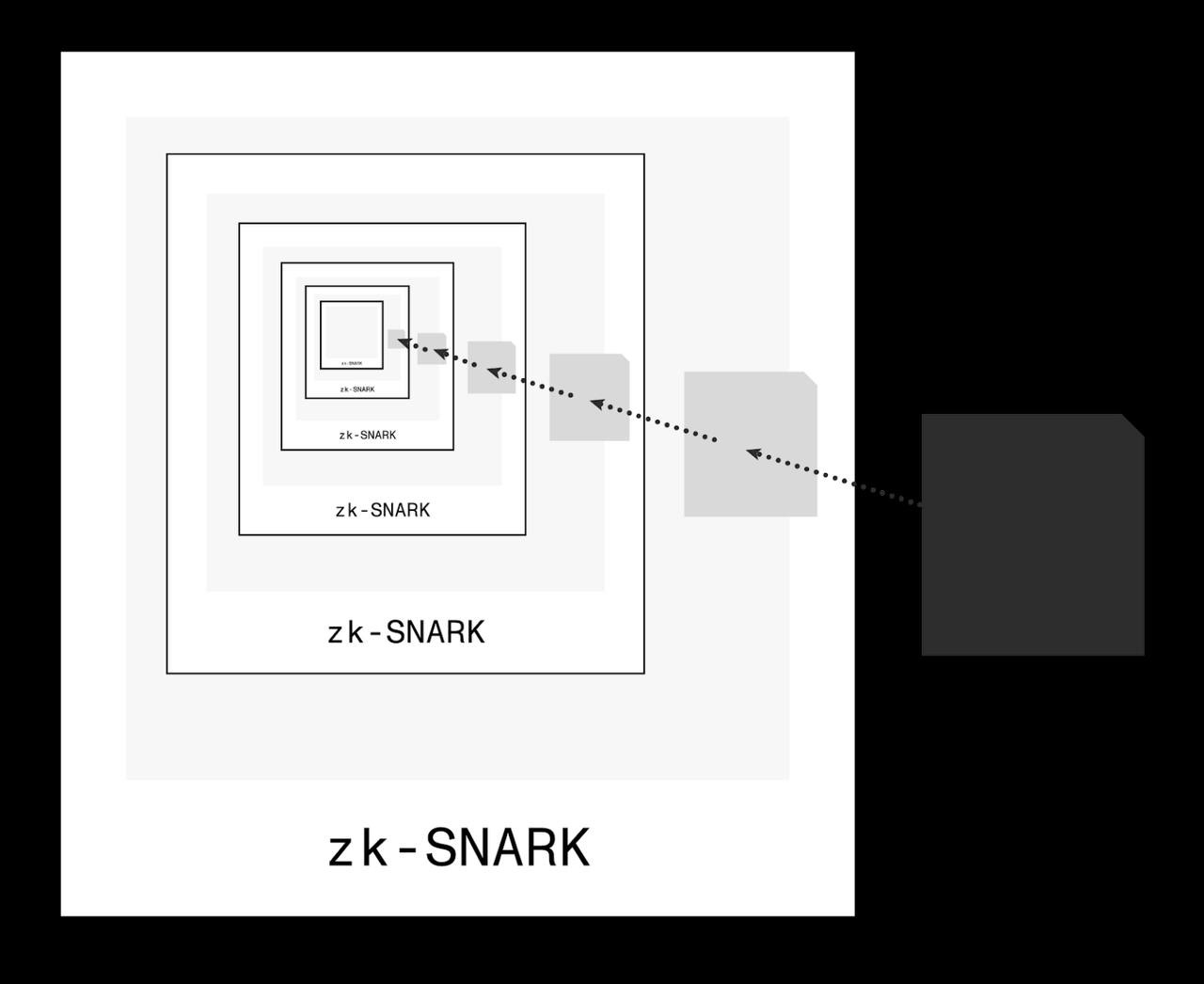
A recursive Zero-Knowledge proof confirms the accuracy of one proof by using that proof to confirm the accuracy of another proof, and so on.
Reasons Why Recursion in ZKP is important
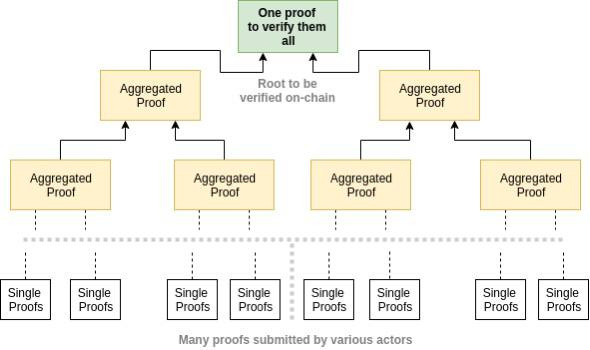
Aggregation
Aggregation is the process of compressing thousands of proofs into a single proof in a blockchain. This not only saves time but also reduces verification costs. It's important to note that this type of proof is only valid if the other constituent proofs are valid as well.
Parallel Proof Generation
Using a standard ZKP, a prover in a rollup releases a single proof to verify, for example, 2,000 transactions sequentially. This process can be time-consuming. However, with Recursive ZKP, a prover can generate 2,000 proofs per transaction, all generated in parallel, as they are independent, making the proving process faster
Incrementally Verifiable Computation (IVC)
Some types of computations need proofs that are incrementally updatable in order to be proved efficiently.
For the context, proofs that are incrementally updatable prove the correctness of a computation, where the proof can be updated or modified as new information is added. Instead of having to start the proof from the beginning every time, the proof can be built upon and extended in small steps, allowing for more efficient and less resource-intensive proving. In other words, an incrementally updatable proof is a proof that can be modified by adding new information to it, rather than having to rebuild it from scratch
Two types of computations
1. Long Computation: proving a long computation requires a lot of memory in the prover side, and in some cases, the computation can’t even fit in the memory, making proving impossible.
2. Evolving Computation: Blockchains that constantly grow need proofs that are incrementally updatable in order to prove the state of the blockchain by validating not only the new blocks but the existing proofs.
This is achieved by breaking the computation into smaller steps and proving them iteratively using recursive zero-knowledge proof specifically IVC. Unlike a standard ZKP, which requires recomputing from the very first step, using a recursive proof, a new proof can be generated for the next step by using the current step and its proof recursively.
How it works with Snarks (Recursive Snark)
ZKPs such as Snarks, which is a ZKP algorithm or proof system, can verify arbitrary computations. An arbitrary computation is one that can be performed using any method or algorithm, rather than a specific, predetermined one, and is not limited to any rule or constraint. Snarks can verify other Snark proofs because verifying a Snark is a computation itself and can be an arbitrary computation. A recursive Snark proof proves the existence of a previous proof that is valid. For a computation to be proved by a Snark, it has to be written in an arithmetic circuit.
Overall, Recursive Zero-Knowledge Proofs provide an efficient and secure way to verify the accuracy of proofs and computations, making it useful in various applications such as blockchain technology.